中学数学纠错笔记——铅直高模型

　　中学数学纠错笔记——铅直高模型

　　实用度：★★★★★

　　平面直角坐标系里，随机的三个点，围成一个三角形，你能求出这个三角形的面积吗？

　　这种题很容易，简单几个字：水平宽乘铅直高

　　打个比方，这道题，随便找三个点A、B、C（坐标看网格），求△ABC 的面积

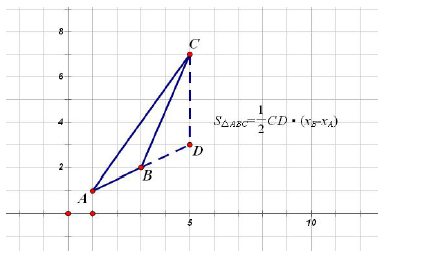
　　好的我们先做辅助线，作CD⊥x 轴交AB（或它的延长线）于D，那么不论这个三角形是钝

　　角三角形还是锐角三角形还是直角三角形，它的面积总会等于图上那玩意。

　　其中，因为CD 是作x 轴的垂线做出来的，所以叫做铅直高，铅直高与哪个边相交，那么这

　　条边（注意是线段，如图的AB）两个端点的水平距离为水平宽（事实上就是右边端点的横

　　坐标减去左边端点的横坐标），两个的乘积的二分之一就是面积，从图上直观地看出，面积

　　是4

　　怎么考？

　　一般让你求一个关于面积的函数解析式，然后求最大值。

　　怎么求？

　　水平宽好求，铅直高呢？再如图：

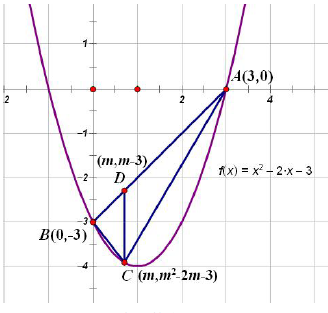
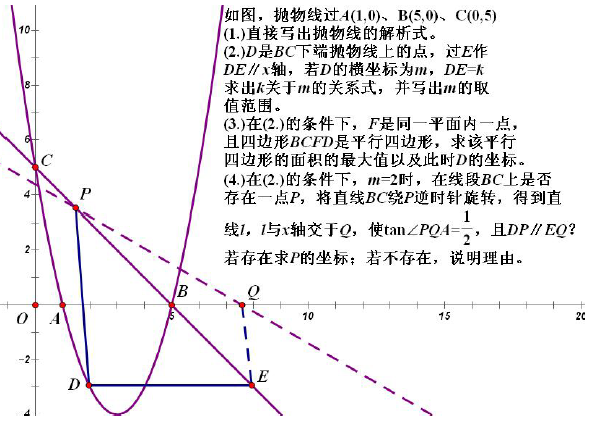
　　好了，已知抛物线函数表达式，如图，C 是AB 下方抛物线上的动点，求△ABC 面积的最

　　大值。做这种题先作辅助线CD⊥x 轴交AB 于D，然后设C 坐标，因为CD⊥x 轴，所以D

　　的横坐标与 C 的相同。所以 CD 的长度就有，拿m . 3 . (m2 . 2m . 3)就是纵坐标相减（注

　　意：被减数一定要是位于上方的点的纵坐标。）

　　这种题近几年考了很多，都快考烂了，所以中考绝不可能出这样常规的题，一定会加以创新。

　　【例题1】（原创）难度：★★★★